1.
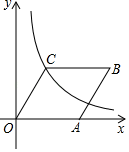
如图,大坝横截面的迎水坡AB的坡比为1:2,即BC:AC=1:2,若坡面AB的水平宽度AC为12米,则斜坡AB的长为( )

A.
4 米
B.
6
米
B.
6 米
C.
6
米
C.
6 米
D.
24米
米
D.
24米
【考点】
勾股定理;