1.
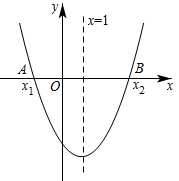
抛物线y=ax2+bx+c（a≠0，a、b、c为常数）与x轴的交点分别是(−1，0)，(3，0) ，下列结论：①4ac−b2>0；②3a+c=0；③当a<0时，若直线y=2与已知抛物线有交点，则a<-
；④若关于x的方程ax2+bx+c−m=0（m>0，m为实数）的一个根为−3，则一定存在一个实数n(0<n<m)，使得关于x的方程ax2+bx+c−n=0有一个整数解为4．其中正确的个数有（ ）
A.
1个
B.
2个
C.
3个
D.
4个
【考点】
二次函数图象与系数的关系;
二次函数图象与坐标轴的交点问题;
