1.
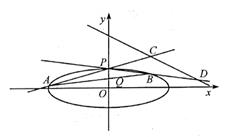
已知椭圆 的左顶点为
的左顶点为 , 左、右焦点分别为
, 左、右焦点分别为 , 过点
, 过点 的直线与椭圆相交于
的直线与椭圆相交于 两点,则( )
两点,则( )
A.
 B.
B.
 C.
当
C.
当 不共线时,
不共线时, 的周长为
的周长为 D.
设点
D.
设点 到直线
到直线 的距离为
的距离为 , 则
, 则
【考点】
直线与圆锥曲线的综合问题;
基础巩固
能力提升
变式训练
拓展培优
真题演练