1.
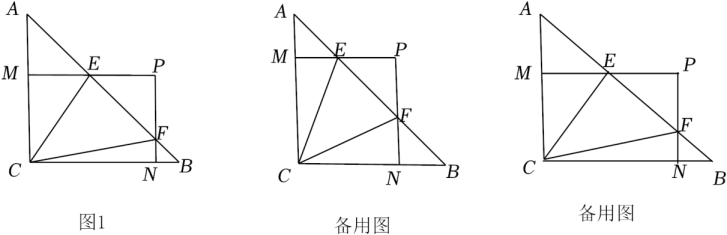
对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形 , 对角线
, 对角线 ,
,  交于点
交于点 .
.

(1)
若 ,
,  ,
,  ,
,  , 请求出
, 请求出 ,
,  ,
,  ,
,  的值.
(2)
若
的值.
(2)
若 ,
,  , 求
, 求 的值.
(3)
请根据(1)(2)题中的信息,写出关于“垂美”四边形关于边的一条结论.
的值.
(3)
请根据(1)(2)题中的信息,写出关于“垂美”四边形关于边的一条结论.
【考点】
勾股定理;
四边形的综合;