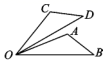
1.
如图,要测量池塘两岸相对的两点 、
、 间的距离,作线段
间的距离,作线段 与
与 相交于点
相交于点 , 使
, 使 ,
,  , 只要测得
, 只要测得 、
、 之间的距离,就可知道
之间的距离,就可知道 、
、 间的距离,此方案依据的数学定理或基本事实是(填
间的距离,此方案依据的数学定理或基本事实是(填 、
、 、
、 、
、 中的一种).
中的一种).

【考点】
三角形全等的判定-SAS;