1.
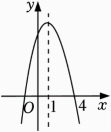
已知关于x的一元二次方程x2+mx+n=0的两个实数根分别为x1=-1,x2=2 ,则二次函数y=x2+mx+n中,当y<0时,x的取值范围是;
【考点】
二次函数与一元二次方程的综合应用;
基础巩固
能力提升
变式训练
拓展培优
真题演练