已知，AC∥ED，∠C=26°，∠CBE=37°，则∠BED的度数是（）

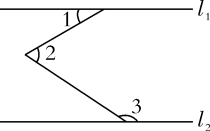
1. 已知，AC∥ED，∠C=26°，∠CBE=37°，则∠BED的度数是（）

A. 53° B. 63° C. 73° D. 83°

【考点】

平行线的判定与性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

单选题容易

1. 嘉嘉在证明“平行于同一条直线的两条直线平行”时，给出了如下的证明过程，淇淇为保证嘉嘉的证明更严谨，想在“ $\text{[math]}$ $\text{[math]}$ ”和“ $\text{[math]}$ $\text{[math]}$ ”之间作补充，下列说法正确的是（）

已知：如图， $\text{[math]}$ ， $\text{[math]}$ ．

求证： $\text{[math]}$ ．

证明：作直线 $\text{[math]}$ 分别交直线 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．

∵ $\text{[math]}$ ， $\text{[math]}$ ．

又∵ $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．

A. 嘉嘉的证明严谨，不需要补充 B. 应补充“ $\text{[math]}$ $\text{[math]}$ ” C. 应补充“ $\text{[math]}$ $\text{[math]}$ ” D. 应补充“ $\text{[math]}$ $\text{[math]}$ ”

单选题容易

2. 如图，下列推理及括号中所注明的推理依据错误的是（）

A. $\text{[math]}$ $\text{[math]}$ （内错角相等，两直线平行） B. $\text{[math]}$ $\text{[math]}$ （两直线平行，内错角相等） C. $\text{[math]}$ $\text{[math]}$ （同旁内角互补，两直线平行） D. $\text{[math]}$ $\text{[math]}$ （两直线平行，同位角相等）

单选题容易

3. 如图，在平行线l₁、l₂之间放置一块直角三角板，三角板的锐角顶点A，B分别在直线l₁、l₂上，若∠1=65°，则∠2的度数是（　　）

A. 25° B. 35° C. 45° D. 65°

单选题容易