1.
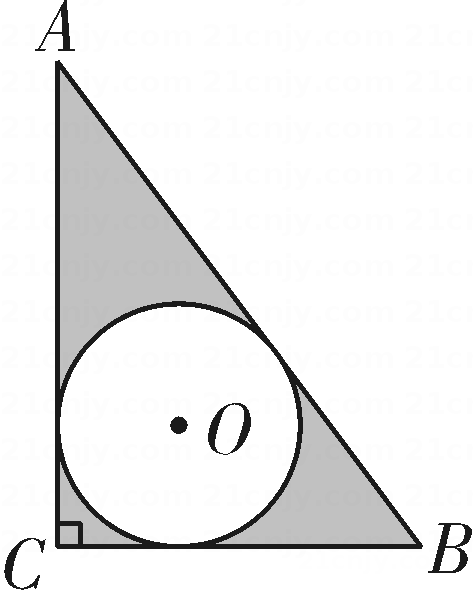
《九章算术》卷九中记载:“今有勾三步,股四步,问勾中容圆径几何?”其大意是:“今有直角三角形勾(短直角边)长为3步,股(长直角边)长为4步,问该直角三角形能容纳的圆(内切圆)的半径是多少步?”如图是示意图,根据题意,该内切圆的半径为.

【考点】
三角形的内切圆与内心;
能力提升
变式训练
拓展培优
真题演练