1.
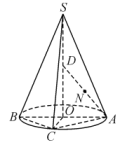
如图,在棱长为 的正方体
的正方体 中,
中, 为
为 的中点,
的中点, 为
为 的中点,如图所示建立空间直角坐标系,则下列说法正确的是( )
的中点,如图所示建立空间直角坐标系,则下列说法正确的是( )

A.
 B.
向量
B.
向量 与
与 所成角的余弦值为
所成角的余弦值为 C.
平面
C.
平面 的一个法向量是
的一个法向量是 D.
点
D.
点 到平面
到平面 的距离为
的距离为
【考点】
空间向量的夹角与距离求解公式;
平面的法向量;