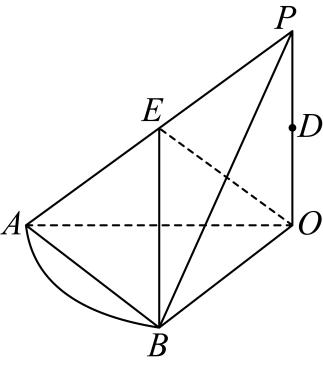
1.
在四棱柱 中,已知
中,已知 平面
平面 ,
,  ,
,  ,
,  ,
,  ,
,  是线段
是线段 上的点.
上的点.

(1)
点 到平面
到平面 的距离;
(2)
若
的距离;
(2)
若 为
为 的中点,求异面直线
的中点,求异面直线 与
与 所成角的余弦值;
(3)
在线段
所成角的余弦值;
(3)
在线段 上是否存在点
上是否存在点 , 使得二面角
, 使得二面角 的余弦值为
的余弦值为 ?若存在,请确定
?若存在,请确定
点位置;若不存在,试说明理由.
【考点】
空间向量的夹角与距离求解公式;
平面的法向量;
用空间向量研究直线与平面所成的角;
用空间向量研究二面角;