1.
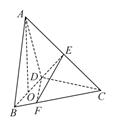
三棱锥 中,
中, ,
,  ,
,  ,
,  .
.

(1)
求平面 和平面
和平面 夹角的余弦值;
(2)
点
夹角的余弦值;
(2)
点 为棱
为棱 (不含端点)上的动点,求直线
(不含端点)上的动点,求直线 与平面
与平面 所成角的正弦值的取值范围.
所成角的正弦值的取值范围.
【考点】
用空间向量研究直线与平面所成的角;
用空间向量研究二面角;
能力提升
真题演练