1.
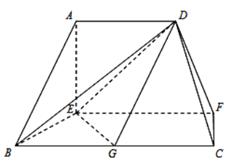
如图,在四棱锥 中,
中, 平面
平面

 ,
,  .
.

(1)
求二面角 的正弦值;
(2)
在棱
的正弦值;
(2)
在棱 上确定一点
上确定一点 , 使异面直线
, 使异面直线 与
与 所成角的大小为
所成角的大小为 , 并求此时点
, 并求此时点 到平面
到平面 的距离.
的距离.
【考点】
空间向量的夹角与距离求解公式;
用空间向量研究二面角;