1.
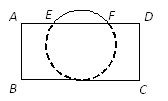
如图,一根长为 的牙刷置于底面直径为
的牙刷置于底面直径为 、高为
、高为 的圆柱形水杯中,牙刷露在杯子外面的长度
的圆柱形水杯中,牙刷露在杯子外面的长度 , 则
, 则 的取值范围是.
的取值范围是.

【考点】
勾股定理的应用;
基础巩固
能力提升
变式训练
拓展培优
真题演练