1.
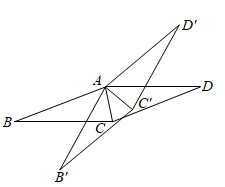
如图所示,把一个直角三角尺ACB绕着30°角的顶点B顺时针旋转,使得点A与CB的延长线上的点E重合.
\
(1)三角尺旋转了 度.
(2)连接CD,试判断△CBD的形状;
(3)求∠BDC的度数.
【考点】
旋转的性质;
基础巩固
能力提升
变式训练
拓展培优
真题演练