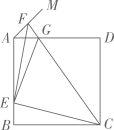
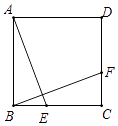
1.
如图, ,
,  , 点
, 点 ,
,  ,
,  在同一直线上,请添加一个条件___________,运用“HL”判定定理,使得
在同一直线上,请添加一个条件___________,运用“HL”判定定理,使得 , 并写出证明过程.
, 并写出证明过程.

【考点】
三角形全等的判定;
基础巩固
能力提升
变式训练
拓展培优
真题演练