1.
下面是小石设计的“过圆上一点作圆的切线”的尺规作图的过程.
已知:如图1,⊙及⊙
上一点
.
求作:直线PN,使得PN与⊙相切.
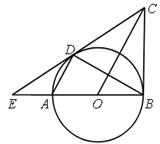
作法:如图2,
①作射线OP;
②在⊙外取一点Q(点Q不在射线OP上),以Q为圆心,QP为半径作圆,⊙Q与射线OP交于另一点M;
③连接MQ并延长交⊙Q于点N;
④作直线PN.
所以直线PN即为所求作直线.
根据小石设计的尺规作图的过程,
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:∵是⊙
的直径,
∴=
( )(填推理的依据).
∴ .
又∵是⊙
的半径,
∴是⊙
的切线( )(填推理的依据).

【考点】
圆周角定理;
切线的判定;
基础巩固
能力提升
变式训练
拓展培优
真题演练






 图2
图2