1.
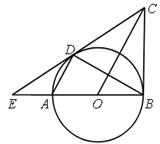
如图,AB为⊙O的直径,BC为⊙O的切线,弦AD∥OC , 直线CD交BA的延长线于点E , 连接BD . 下列结论:①CD是⊙O的切线;②CO⊥DB;③△EDA∽△EBD;④ED·BC=BO·BE . 其中正确结论的个数有( )
A.
4个
B.
3个
C.
2个
D.
1个
【考点】
全等三角形的判定与性质;
圆周角定理;
切线的判定;
相似三角形的判定与性质;