1.
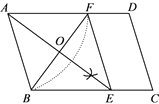
如图,以BC为直径的⊙O交△CFB的边CF于点A,BM平分∠ABC交AC于点M,AD⊥BC于点D,AD交BM于点N,ME⊥BC于点E,AB2=AF·AC,cos∠ABD=  ,AD=12.
,AD=12.

(1)
求证:△ABF∽△ACB;
(2)
求证:FB是⊙O的切线;
(3)
证明四边形AMEN是菱形,并求该菱形的面积S.
【考点】
全等三角形的判定与性质;
菱形的判定与性质;
圆周角定理;
切线的判定;
相似三角形的判定与性质;