1.
已知y是关于x的一次函数,下表列出了这个函数部分的对应值:

(1)求这个一次函数的表达式.
(2)求m,n的值.
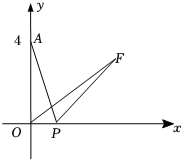
(3)已知点和点
在该一次函数图象上,设
, 判断正比例函数
的图象是否有可能经过第一象限,并说明理由.
【考点】
待定系数法求一次函数解析式;
基础巩固
能力提升
变式训练
拓展培优
真题演练