1.
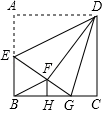
小明家窗外有一个路灯，每天晚上灯光都会透过窗户照进房间里，小明利用相关数学知识测量了这个路灯的高．如图，光线透过窗子
照亮地面的长度为
， 小明测得窗户距离地面高度
， 窗高
， 某一时刻，
， 
， 其中
、
、
、
四点在同一条直线上，
、
、三点在同一条直线上，
， 请求出路灯的高度
．
【考点】
平行线的判定;
相似三角形的判定与性质;
基础巩固
能力提升
变式训练
拓展培优
真题演练
