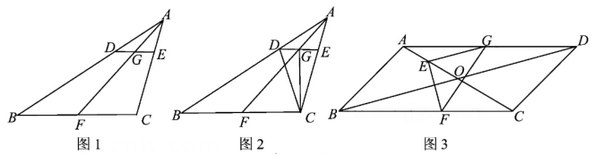
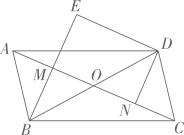
1.
如图,在 中,
中, ,
,  , 在射线
, 在射线 上取一点
上取一点 , 使得
, 使得 . 当点
. 当点 从点
从点 匀速运动到点
匀速运动到点 时,点
时,点 恰好从点
恰好从点 匀速运动到点
匀速运动到点 . 在线段
. 在线段 上取点
上取点 , 使得
, 使得 , 连接
, 连接 , 记
, 记 .
.

(1)
① ______(用含
______(用含 的式子表示);
(2)
若以
的式子表示);
(2)
若以 ,
,  ,
,  ,
,  为顶点的四边形是平行四边形,请求出
为顶点的四边形是平行四边形,请求出 的值.
的值.
②若 , 求
的长.
【考点】
等腰三角形的判定与性质;
平行四边形的性质;