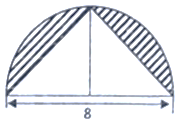
(相似三角形)如图，已知正方形的边长是 12 厘米，是边上的中点，连接对角线，交于点，则三角形的面积是 ( ) 平方厘米。

1. (相似三角形)如图，已知正方形 $\text{[math]}$ 的边长是 12 厘米， $\text{[math]}$ 是 $\text{[math]}$ 边上的中点，连接对角线 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ，则三角形 $\text{[math]}$ 的面积是 ( ) 平方厘米。

A. 24 B. 36 C. 48 D. 60

【考点】

组合图形面积的巧算; 三角形的面积;

【答案】

您现在未登录，无法查看试题答案与解析。登录

单选题普通

1. 我国古代数学名著《九章算术》中记载了三角形面积的计算方法，著名数学家刘徽在注文中用“以盈补虚”的方法（如图）对其加以说明。下面说法中描述错误的是（）

A. 长方形的长等于三角形的高。 B. 长方形的宽等于三角形的底。 C. 三角形底的长度等于长方形两条宽的和。 D. 长方形的面积等于三角形的面积。

单选题容易

2. （三角形的面积）一个三角形的底是3dm，如果底增加1dm，那么三角形的面积就增加1.2dm² ，原来三角形的面积是（）dm²。

A. 0.2 B. 3.6 C. 4.8 D. 7.2

单选题容易

3. 一个直角三角形的三条边长分别是6厘米、8厘米、10厘米，那么它的面积是（）平方厘米。

A. 10×8÷2 B. 6×10÷2 C. 6×8÷2 D. 6×10

单选题容易