1.
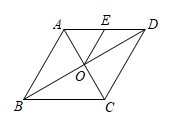
如图,在平面直角坐标系xOy中,Rt△OAB的直角顶点A在x轴上,∠B=30°,反比例函数y= (k≠0)在第一象限的图象经过OB边上的点C和AB的中点D,连接AC.已知S△OAC=4
(k≠0)在第一象限的图象经过OB边上的点C和AB的中点D,连接AC.已知S△OAC=4 , 则实数k的值为( )
, 则实数k的值为( )

A.
4 B.
6
B.
6 C.
8
C.
8 D.
10
D.
10
【考点】
含30°角的直角三角形;
勾股定理;
基础巩固
能力提升
变式训练
拓展培优
真题演练