1.
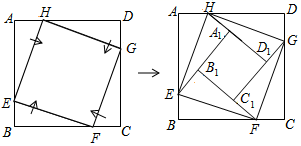
如图,五个全等的小正方形无缝隙、不重合地拼成了一个“十字”形,连接A、B两个顶点,过顶点C作CD⊥AB,垂足为D.“十字”形被分割为了①、②、③三个部分,这三个部分恰好可以无缝隙、不重合地拼成一个矩形,这个矩形的长与宽的比值为.

【考点】
正方形的判定与性质;
基础巩固
能力提升
变式训练
拓展培优
真题演练