1.
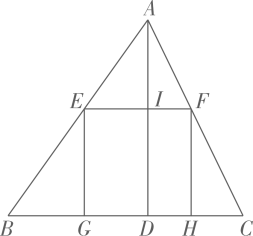
如图,某校教学楼 的楼顶
的楼顶 处有一盏照明灯,教学楼前有三棵高度均为
处有一盏照明灯,教学楼前有三棵高度均为 的小树
的小树 、
、 、
、 . 某天晚上,当照明灯
. 某天晚上,当照明灯 打开后,小树
打开后,小树 的影子为
的影子为 , 小树
, 小树 的影子顶端恰好在小树
的影子顶端恰好在小树 的底部
的底部 处,通过测量可得
处,通过测量可得 ,
,  , 已知
, 已知 ,
,  ,
,  , 点
, 点 在同一条直线上,请你计算教学楼的高度
在同一条直线上,请你计算教学楼的高度 .
.

【考点】
相似三角形的判定与性质;
相似三角形的应用;
基础巩固
能力提升
变式训练
拓展培优
真题演练