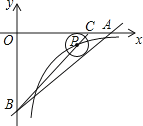
如图所示，在平面直角坐标系中，过格点，，作一圆弧，在第一象限，过点B与格点（填点的坐标）的直线与该圆弧相切．

0 返回首页

1. 如图所示，在平面直角坐标系中，过格点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 作一圆弧，在第一象限，过点B与格点（填点的坐标）的直线与该圆弧相切．

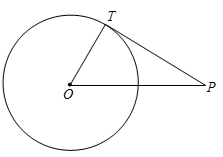
【考点】

切线的性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

填空题容易

基础巩固

能力提升

变式训练

拓展培优

真题演练

换一批

1. 如图， $\text{[math]}$ 是 $\text{[math]}$ 的直径， $\text{[math]}$ 是 $\text{[math]}$ 上的点，过点 $\text{[math]}$ 作 $\text{[math]}$ 的切线交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ．若 $\text{[math]}$ ，则 $\text{[math]}$ 度．

填空题容易

2. 以 $\text{[math]}$ 为中心点的量角器与直角三角板 $\text{[math]}$ 如图所示摆放，直角顶点 $\text{[math]}$ 在零刻度线所在直线 $\text{[math]}$ 上，且量角器与三角板只有一个公共点 $\text{[math]}$ ，若点 $\text{[math]}$ 的读数为135°，则 $\text{[math]}$ 的度数是．

填空题容易

3. 如图， $\text{[math]}$ 是 $\text{[math]}$ 的切线， $\text{[math]}$ 是切点．若 $\text{[math]}$ ，则 $\text{[math]}$ ．

填空题容易

1. 如图，点 $\text{[math]}$ 为 $\text{[math]}$ 轴上一点，点C在函数 $\text{[math]}$ 的图象上， $\text{[math]}$ 轴切 $\text{[math]}$ 于点 $\text{[math]}$ ．若 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 三点恰好在同一直线上， $\text{[math]}$ 的面积为 $\text{[math]}$ ，则 $\text{[math]}$ 的值为．

填空题普通

2. 如图，在Rt△AOB中，∠AOB＝90°，OA＝3，OB＝4，⊙O的半径为2，点P是AB边上的动点，过点P作⊙O的一条切线PC（点C为切点），则线段PC长的最小值为．

填空题困难

3. 小明用一把角尺和一块边长为3 $\text{[math]}$ 的正方形小木块测量并计算圆的半径，如图，小木块（正方形 $\text{[math]}$ ）两边紧靠在角尺的两边，顶点C紧靠 $\text{[math]}$ 上，角尺的较长边与 $\text{[math]}$ 相切于点E．量得 $\text{[math]}$ ，则 $\text{[math]}$ 的半径等于 $\text{[math]}$ ．

填空题普通

1. 如图，⊙O是以原点为圆心，2 $\text{[math]}$ 为半径的圆，点P是直线y＝－x＋8上的一点，过点P作⊙O的一条切线PQ，Q为切点，则切线长PQ的最小值为（）

A. 2 $\text{[math]}$ B. 4 C. 8－2 $\text{[math]}$ D. 2 $\text{[math]}$

单选题容易

2. 如图，AB与⊙O相切于点B，连结AO并延长交⊙O于点C，连结BC．若∠C=34°，则∠A的度数是(　　)

A. 17° B. 22° C. 34° D. 56°

单选题普通

3. 如图，过⊙O上一点C作⊙O的切线，交⊙O直径AB的延长线于点D．若∠D＝40°，则∠A的度数为（　　）

A. 20° B. 25° C. 30° D. 40°

单选题容易

1. 在平面直角坐标系 $\text{[math]}$ 中，将对角线交点为 $\text{[math]}$ 的正方形记作正方形 $\text{[math]}$ ，对于正方形 $\text{[math]}$ 和点 $\text{[math]}$ （不与 $\text{[math]}$ 重合）给出如下定义：若正方形 $\text{[math]}$ 的边上存在点 $\text{[math]}$ ，使得直线 $\text{[math]}$ 与以 $\text{[math]}$ 为半径的 $\text{[math]}$ 切于点 $\text{[math]}$ ，则称点 $\text{[math]}$ 为正方形 $\text{[math]}$ 的“伴随切点”．

(1) 如图，正方形 $\text{[math]}$ 的顶点分别为点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．

$\text{[math]}$ 在点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 中，正方形 $\text{[math]}$ 的“伴随切点”是________；

$\text{[math]}$ 若直线 $\text{[math]}$ 上存在正方形 $\text{[math]}$ 的“伴随切点”，求 $\text{[math]}$ 的取值范围；

(2) 已知点 $\text{[math]}$ ，正方形 $\text{[math]}$ 的边长为 $\text{[math]}$ ．若存在正方形 $\text{[math]}$ 的两个“伴随切点” $\text{[math]}$ ， $\text{[math]}$ ，使得 $\text{[math]}$ 为等边三角形，直接写出 $\text{[math]}$ 的取值范围．

解答题困难

2. 对于平面直角坐标系 $\text{[math]}$ 中的点 $\text{[math]}$ 和图形 $\text{[math]}$ ，给出如下的定义：若在图形 $\text{[math]}$ 上存在一点 $\text{[math]}$ ，使得 $\text{[math]}$ 两点间的距离小于或等于 $\text{[math]}$ ，则称 $\text{[math]}$ 为图形 $\text{[math]}$ 的关联点．

(1) 当 $\text{[math]}$ 的半径为 $\text{[math]}$ 时，

① 在点 $\text{[math]}$ 中， $\text{[math]}$ 的关联点是_______；

② 点 $\text{[math]}$ 在直线 $\text{[math]}$ 上，若 $\text{[math]}$ 为 $\text{[math]}$ 的关联点，直接写出点 $\text{[math]}$ 的横坐标 $\text{[math]}$ 的取值范围；

(2) $\text{[math]}$ 的圆心在 $\text{[math]}$ 轴上，半径为 $\text{[math]}$ ，直线 $\text{[math]}$ 与 $\text{[math]}$ 轴， $\text{[math]}$ 轴分别交于点 $\text{[math]}$ ．若线段 $\text{[math]}$ 上的所有点都是 $\text{[math]}$ 的关联点，直接写出圆心 $\text{[math]}$ 的横坐标 $\text{[math]}$ 的取值范围．

解答题困难

3. 在平面直角坐标系 $\text{[math]}$ 中， $\text{[math]}$ 的半径为1．对于 $\text{[math]}$ 的弦 $\text{[math]}$ 和一点 $\text{[math]}$ ，给出如下定义：若直线 $\text{[math]}$ 与 $\text{[math]}$ 只有一个公共点， $\text{[math]}$ ，则称点 $\text{[math]}$ 是弦 $\text{[math]}$ 的“ $\text{[math]}$ 切割点”．

(1) 已知点 $\text{[math]}$ ．

①若点 $\text{[math]}$ 为弦 $\text{[math]}$ 的“ $\text{[math]}$ 切割点”，则 $\text{[math]}$ ______，点 $\text{[math]}$ 的坐标为______；

②若弦 $\text{[math]}$ 与 $\text{[math]}$ 轴平行且只有一个点 $\text{[math]}$ 为弦 $\text{[math]}$ 的“ $\text{[math]}$ 切割点”，则 $\text{[math]}$ 的取值范围是______；

(2) 已知点 $\text{[math]}$ 为直线 $\text{[math]}$ 上一点，若存在 $\text{[math]}$ 的弦 $\text{[math]}$ ．当 $\text{[math]}$ 时，点 $\text{[math]}$ 为弦 $\text{[math]}$ 的“ $\text{[math]}$ 切割点”．直接写出 $\text{[math]}$ 的取值范围．

解答题困难

如图，OA在x轴上，OB在y轴上，OA=8，AB=10，点C在边OA上，AC=2，⊙P的圆心P在线段BC上，且⊙P与边AB，AO都相切．若反比例函数y= $\text{[math]}$ （k≠0）的图象经过圆心P，则k= ．

填空题困难

2. 如图，等边△ABC的周长为6π，半径是1的⊙O从与AB相切于点D的位置出发，在△ABC外部按顺时针方向沿三角形滚动，又回到与AB相切于点D的位置，则⊙O自转了（）

A. 2周 B. 3周 C. 4周 D. 5周

单选题普通

3. 如图，已知⊙O的半径为1，点P是⊙O外一点，且OP=2。若PT是⊙O的切线，T为切点，连结OT，则PT=

填空题普通