1.
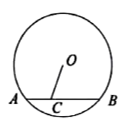
如图是一位同学从照片上剪切下来的海上日出时的画面，“图上”太阳与海平线交于
， 
两点，他测得“图上”圆的半径为10厘米，
厘米．若从目前太阳所处位置到太阳完全跳出海平面的时间为16分钟，则“图上”太阳升起的速度为（ ）
A.
1.0厘米/分
B.
0.8厘米/分
C.
1.2厘米/分
D.
1.4厘米/分
【考点】
勾股定理;
垂径定理的实际应用;
