1.
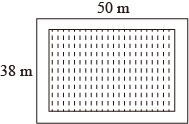
在长为 , 宽为
, 宽为 的长方形田地中开辟三条宽度相等的道路,已知剩余田地的面积为
的长方形田地中开辟三条宽度相等的道路,已知剩余田地的面积为 , 求道路的宽度.设道路的宽度为
, 求道路的宽度.设道路的宽度为 , 则可列方程( )
, 则可列方程( )

A.
 B.
B.
 C.
C.
 D.
D.

【考点】
一元二次方程的应用-几何问题;
基础巩固
能力提升
变式训练
拓展培优
真题演练