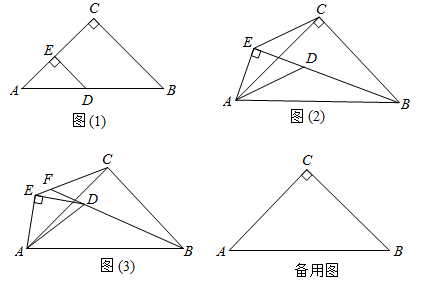
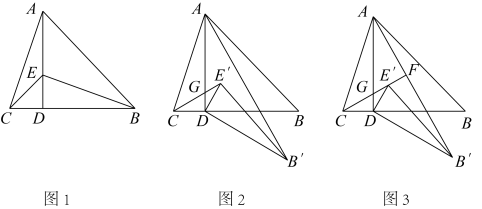
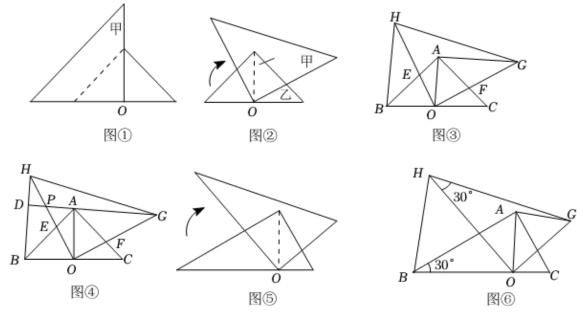
【问题情景】如图，在△ABC，中，∠BAC=90°，AB=AC，AD是BC边上的高，点E是边AB上的一动点（不与点A，B重合），连接CE交AD于点F，将线段CF绕点C顺时针旋转得到线段CG，连接AG.

0 返回首页

1. 【问题情景】如图，在△ABC，中，∠BAC=90°，AB=AC，AD是BC边上的高，点E是边AB上的一动点（不与点A，B重合），连接CE交AD于点F，将线段CF绕点C顺时针旋转 $\text{[math]}$ 得到线段CG，连接AG.

(1) 如图1，当CE是∠ACB的角平分线时

①求证：AE=AF；

②直接写出∠CAG= .

(2) 【深入探究】

依题意补全图2，用等式表示线段AF，AC，AG之间的数量关系，并证明.

【考点】

旋转的性质; 三角形的综合;

【答案】

您现在未登录，无法查看试题答案与解析。登录

实践探究题困难

(1) 观察猜想

小华将△ADE绕点A逆时针旋转，连接 $\text{[math]}$ ，如图（2），当 $\text{[math]}$ 的延长线恰好经过点E时，

① $\text{[math]}$ 的值为；

② $\text{[math]}$ 的度数为度；

(2) 类比探究

如图（3），小芳在小华的基础上，继续旋转△ADE，连接 $\text{[math]}$ ，设 $\text{[math]}$ 的延长线交 $\text{[math]}$ 于点F ，请求出 $\text{[math]}$ 的值及 $\text{[math]}$ 的度数，并说明理由．

(3) 拓展延伸

若 $\text{[math]}$ ，当 $\text{[math]}$ 所在的直线垂直于 $\text{[math]}$ 时，请你直接写出 $\text{[math]}$ 的长．

实践探究题困难

2. 问题提出

如图（ $\text{[math]}$ ），在 $\text{[math]}$ 和 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 内部，直线 $\text{[math]}$ 与 $\text{[math]}$ 交于点 $\text{[math]}$ ．线段 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间存在怎样的数量关系？

(1) 问题探究：

①先将问题特殊化如图（ $\text{[math]}$ ），当点 $\text{[math]}$ ， $\text{[math]}$ 重合时，易证 $\text{[math]}$ （ $\text{[math]}$ ），请利用全等探究 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间的数量关系（直接写出结果，不要求写出理由）；

②再探究一般情形如图（ $\text{[math]}$ ），当点 $\text{[math]}$ ， $\text{[math]}$ 不重合时，证明（ $\text{[math]}$ ）中的结论仍然成立．

(2) 问题拓展：

如图（ $\text{[math]}$ ），在 $\text{[math]}$ 和 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ （ $\text{[math]}$ 是常数），点 $\text{[math]}$ 在 $\text{[math]}$ 内部，直线 $\text{[math]}$ 与 $\text{[math]}$ 交于点 $\text{[math]}$ ．直接写出一个等式，表示 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间的数量关系．

实践探究题困难

(1) 问题背景如图，在等腰△ABC中，AB=AC，∠BAC=a，D为BC边上的一动点，将线段AD绕点A逆时针旋转a得到线段AE，连接CE.求证：BD=CE；

(2) 尝试运用如图，在等腰△ABC中，AB=AC，∠BAC=120°，D为BC边上的一动点，以AD为斜边在AD右侧构造Rt△AMD，∠AMD=90°，∠ADM=30°.连接CM，设BD=a，CD=b，求△CDM的面积（用a，b表示）；

(3) 拓展创新如图，在Rt△BCD中，∠BCD=90°，∠CBD=30°，∠BAD=30°，AB=1， $\text{[math]}$ ，直接写出△ABC的面积.

实践探究题困难