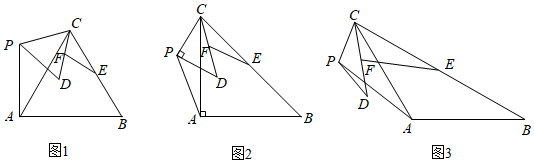
1.
(1)
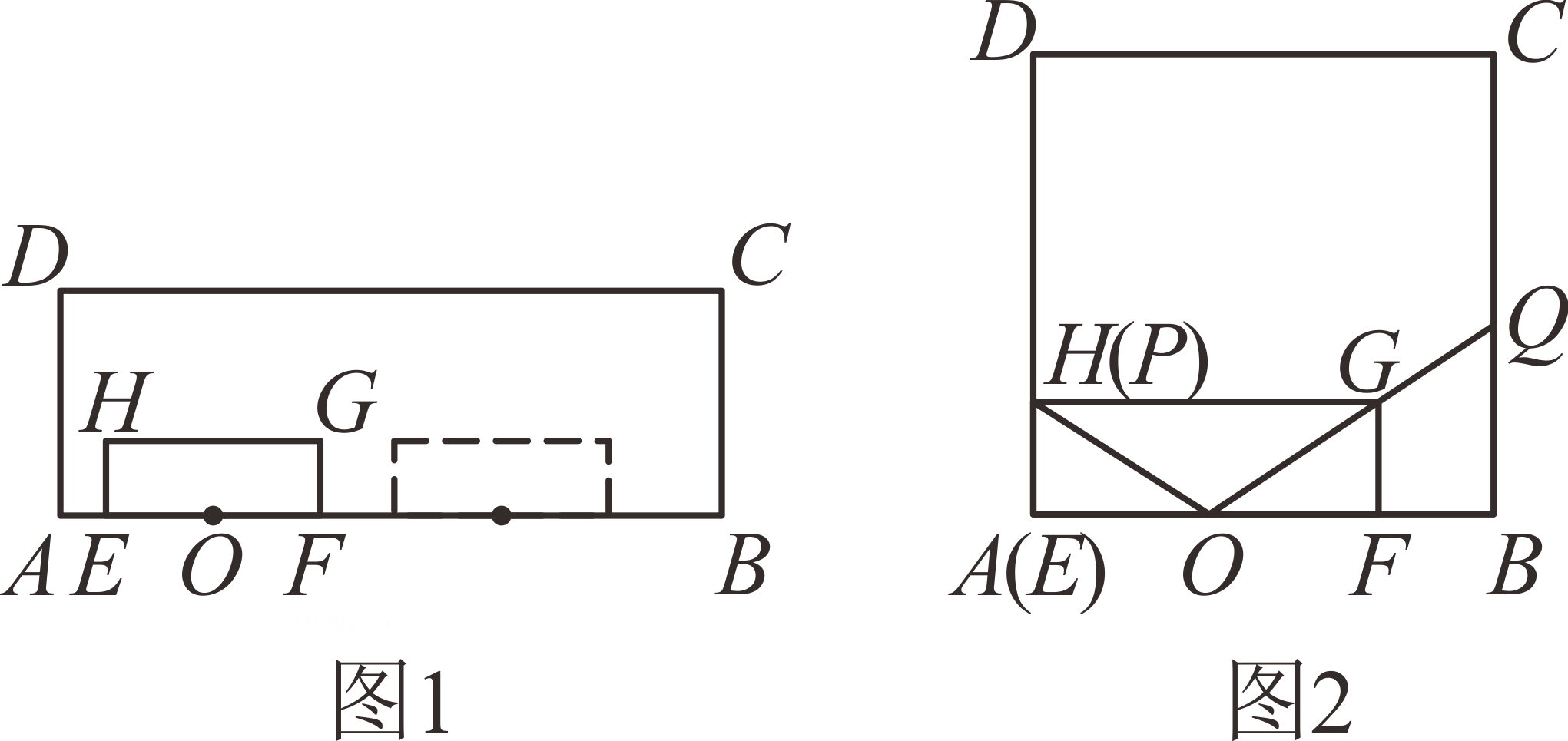
【情境再现】
(2)
【迁移应用】
(3)
【拓展延伸】
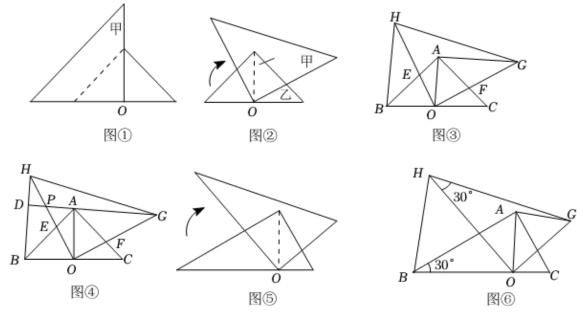
甲、乙两个含角的直角三角尺如图①放置,甲的直角顶点放在乙斜边上的高的垂足O处,将甲绕点O顺时针旋转一个锐角到图②位置.小莹用作图软件Geogebra按图②作出示意图,并连接
, 如图③所示,
交
于E,
交
于F,通过证明
, 可得
.
请你证明: .
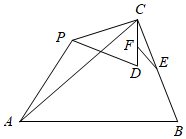
延长分别交
所在直线于点P,D,如图④,猜想并证明
与
的位置关系.
小亮将图②中的甲、乙换成含角的直角三角尺如图⑤,按图⑤作出示意图,并连接
, 如图⑥所示,其他条件不变,请你猜想并证明
与
的数量关系.
【考点】
相似三角形的判定与性质;
旋转的性质;
三角形的综合;
能力提升
真题演练