1.
数学课上，有这样一道探究题．
如图，已知△ABC中，AB=AC=m，BC=n，∠BAC=α（0°＜α＜180°），点P为平面内不与点A、C重合的任意一点，连接CP，将线段CP绕点P顺时针旋转α，得线段PD，连接CD、AP点E、F分别为BC、CD的中点，设直线AP与直线EF相交所成的较小角为β，探究的
的值 和β的度数与m、n、α的关系．
请你参与学习小组的探究过程，并完成以下任务：
如图，已知△ABC中，AB=AC=m，BC=n，∠BAC=α（0°＜α＜180°），点P为平面内不与点A、C重合的任意一点，连接CP，将线段CP绕点P顺时针旋转α，得线段PD，连接CD、AP点E、F分别为BC、CD的中点，设直线AP与直线EF相交所成的较小角为β，探究的
请你参与学习小组的探究过程，并完成以下任务：
(1)
【问题发现】 填空：
(2)
求出
时
的值和
的度数．
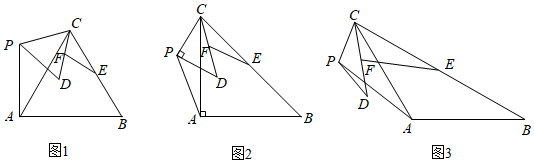
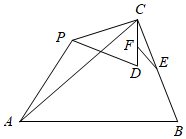
小明研究了α=60°时，如图1，求出了的值 和β的度数分别为
，
；
小红研究了α=90°时，如图2，求出了的值 和β的度数分别为
，
；
【类比探究】
他们又共同研究了α=120°时，如图3，也求出了 的值和β的度数；
【归纳总结】
最后他们终于共同探究得出规律：(用含m、n的式子表示)；
(用含α的式子表示)．
【考点】
相似三角形的判定与性质;
旋转的性质;
三角形的综合;
三角形-动点问题;
能力提升
