1.
在 中,
中, , E , F , D分别是AC , AB , BC上的点,
, E , F , D分别是AC , AB , BC上的点, ,
,  .
.

(1)
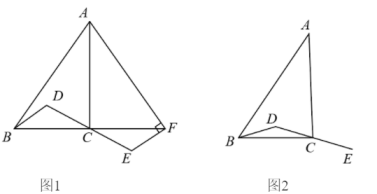
求 的度数(图1);
(2)
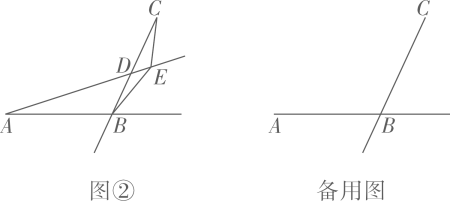
若点G为BC的中点(图2),其它条件不变,请探究FG与EG是否垂直;
(3)
将(1)中
的度数(图1);
(2)
若点G为BC的中点(图2),其它条件不变,请探究FG与EG是否垂直;
(3)
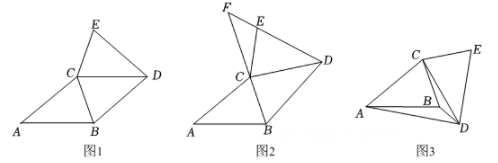
将(1)中 绕点D逆时针旋转一定的角度得到
绕点D逆时针旋转一定的角度得到 , 如图3所示,G为线段
, 如图3所示,G为线段 的中点,
的中点, 吗?请说明理由.
吗?请说明理由.
【考点】
三角形内角和定理;
等腰三角形的性质;
三角形全等的判定-SAS;