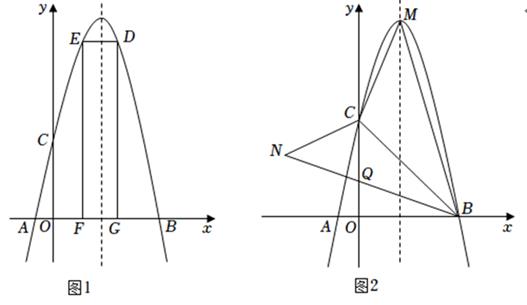
1.
在直角坐标系中,设函数 是常数,
是常数, .
.
(1)
若该函数的图象经过 和
和 两点,求函数的表达式;
(2)
已知
两点,求函数的表达式;
(2)
已知 , 当
, 当 (
( 是实数,
是实数, )时,该函数对应的函数值分别为
)时,该函数对应的函数值分别为 若
若 , 求证:
, 求证: .
.
【考点】
二次函数的最值;
待定系数法求二次函数解析式;