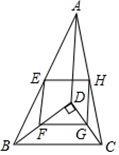1.
勾股定理被誉为 “几何明珠”, 如图 19-12 是我国古代著名的“赵爽弦图”, 它由 4 个全等的直角三角形拼成, 已知大正方形面积为 25 , 小正方形面积为 1 . 若用  表示直角三角形的两直角边的长, 则下列结论不正确的是( )
表示直角三角形的两直角边的长, 则下列结论不正确的是( )

A.
 B.
B.
 C.
C.
 D.
D.

【考点】
勾股定理;
基础巩固
能力提升
变式训练
拓展培优
真题演练