1.
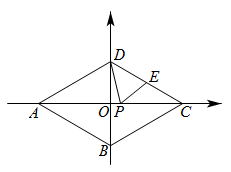
如图, 菱形  , 点
, 点  均在坐标轴上, 且
均在坐标轴上, 且  是
是  的中点,
的中点,  是
是  上的一动点, 则
上的一动点, 则  的最小值是( )
的最小值是( )

A.
3
B.
5
C.
 D.
D.

【考点】
菱形的性质;
轴对称的应用-最短距离问题;
基础巩固
能力提升
变式训练
拓展培优
真题演练