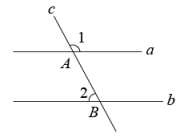
光线在不同介质中传播速度不同，从一种介质射向另一种介质时会发生折射．如图，水面与水杯下沿平行，光线从空气射向水中时发生折射，光线变成，点H在光线所在的直线上，已知，求的度数．

1. 光线在不同介质中传播速度不同，从一种介质射向另一种介质时会发生折射．如图，水面 $\text{[math]}$ 与水杯下沿 $\text{[math]}$ 平行，光线 $\text{[math]}$ 从空气射向水中时发生折射，光线变成 $\text{[math]}$ ，点H在光线 $\text{[math]}$ 所在的直线上，已知 $\text{[math]}$ ，求 $\text{[math]}$ 的度数．

【考点】

平行线的性质; 对顶角及其性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题普通

1. 完成下面的证明：如图，AB 和CD相交于点O，AC//BD，∠A=∠AOC．求证∠B=∠BOD．

证明：∵AC//BD(已知)

∴∠A=∠B（）．

∵∠A=∠AOC(已知)

∴∠B=∠AOC（）．

∵∠AOC=∠ ▲ （）．

∴∠B=∠BOD（等量代换）．

解答题容易

2. 完成证明并写出推理根据：如图，直线 $\text{[math]}$ 分别与直线 $\text{[math]}$ 、 $\text{[math]}$ 交于点 $\text{[math]}$ 和点 $\text{[math]}$ ． $\text{[math]}$ ，射线 $\text{[math]}$ 、 $\text{[math]}$ 分别与直线 $\text{[math]}$ 交于点 $\text{[math]}$ 、 $\text{[math]}$ ，且 $\text{[math]}$ ，则 $\text{[math]}$ 与 $\text{[math]}$ 有何数量关系？并说明理由．

解： $\text{[math]}$ 与 $\text{[math]}$ 的数量关系为　　，理由如下：

$\text{[math]}$ （已知）．

∴ $\text{[math]}$ ∥　　(　　)．

$\text{[math]}$ 　　(　　)．

$\text{[math]}$ （已知），

$\text{[math]}$ 　　 $\text{[math]}$ （垂直的定义）．

$\text{[math]}$ 　　．

$\text{[math]}$ 　　．

证明题容易

3. 如图，AB∥CD∥PN，∠ABC=50°，∠CPN=150°．求∠BCP的度数．

解答题容易