1.
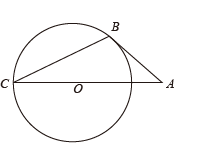
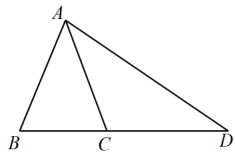
如图,“三等分角器”是由两根有槽的棒PA , PB组成,两根棒在P点相连,并可绕点P转动,C点固定,O , A可在槽内滑动, , 若
, 若 , 则
, 则 的度数为°.
的度数为°.

【考点】
三角形的外角性质;
等腰三角形的性质;
基础巩固
能力提升
变式训练
拓展培优
真题演练