1.
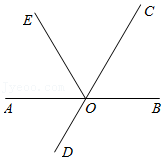
OB是∠AOC内部一条射线,OM是∠AOB平分线,ON是∠AOC平分线,OP是∠NOA平分线,OQ是∠MOA平分线,则∠POQ:∠BOC=( )

A.
1:2
B.
1:3
C.
2:5
D.
1:4
【考点】
角的运算;
角平分线的概念;
基础巩固
能力提升
变式训练
拓展培优
真题演练