1.
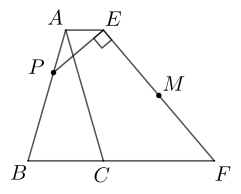
如图,以钝角三角形 的最长边
的最长边 为边外作矩形
为边外作矩形 , 连结
, 连结 ,
,  , 设
, 设 的面积分别为
的面积分别为 , 若要㧔出
, 若要㧔出 的值,只需知道( )
的值,只需知道( )

A.
 的面积
B.
的面积
B.
 的面积
C.
的面积
C.
 的面积
D.
矩形
的面积
D.
矩形 的面积
的面积
【考点】
三角形的面积;
矩形的判定与性质;