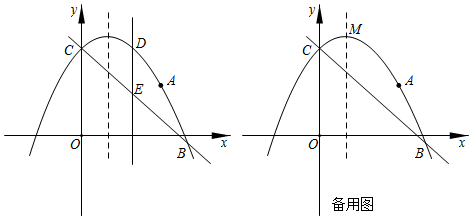
1.
二次函数
 是常数)的图象与
是常数)的图象与 轴交于A,B两点。
轴交于A,B两点。
(1)
若A,B两点的坐标分别为 ,
,  , 求函数
, 求函数 的表达式及其图象的对称轴;
(2)
若函数
的表达式及其图象的对称轴;
(2)
若函数 的图象经过点
的图象经过点 , 且
, 且 时,求
时,求 的最大值;
(3)
若一次函数
的最大值;
(3)
若一次函数 是常数,
是常数,
 , 它的图象与
, 它的图象与 的图象都经过
的图象都经过 轴上同一点,且
轴上同一点,且 .当函数
.当函数 的图象与
的图象与 轴仅有一个交点时,求
轴仅有一个交点时,求 的值.
的值.
【考点】
二次函数的最值;
待定系数法求二次函数解析式;
二次函数y=ax²+bx+c的性质;
能力提升
真题演练