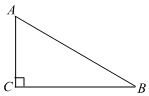
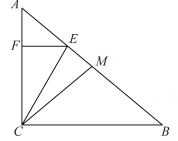
如图，在△ABC中，∠BCA＝90°， AC=8， sinB＝，点D是斜边AB的中点，点E是边AC的中点，连接CD，点P为线段CD上一点，作点C关于直线EP对称点F，连结EF、PF，设DP长为x（x＞0）．

1. 如图，在△ABC中，∠BCA＝90°， AC=8， sinB＝ $\text{[math]}$ ，点D是斜边AB的中点，点E是边AC的中点，连接CD，点P为线段CD上一点，作点C关于直线EP对称点F，连结EF、PF，设DP长为x（x＞0）．

(1) AB的长为．

(2) 求PF长度（用含x的代数式表示）．

(3) 当点F落在直线CD上时，求x的值．

(4) 当直线PF与△ABC的边BC或AC垂直时，直接写出x的值．

【考点】

解直角三角形; 直角三角形斜边上的中线;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题困难

1. 如图，在△ABC中，BC=12，tanA= $\text{[math]}$ ，∠B=30°；求AC和AB的长．

解答题普通

2. 如图，在Rt△ABC中，∠C＝90°，BC＝2，AC＝2 $\text{[math]}$ ．解这个直角三角形．

解答题普通

3. 小星手中有一把残缺的刻度尺，他想知道其宽度 $\text{[math]}$ ，但手中只有一把刻度模糊的 $\text{[math]}$ 直角三角板，无法直接测量，于是他将直角三角板锐角顶点与尺下沿的端点A重合，斜边与尺下沿 $\text{[math]}$ 重合，如图①，一直角边与尺上沿的交点B在尺上的读数即为直尺的宽．

(1) 【实践探究】小红受到小星的启发，将 $\text{[math]}$ 的 $\text{[math]}$ 按小星的方式放置在一把残缺的刻度尺上，如图②， $\text{[math]}$ 与尺上沿的交点B在尺上的读数恰为3厘米，求该刻度尺的宽度 $\text{[math]}$ 的长；

(2) 【问题解决】小红继续按相同的方式将 $\text{[math]}$ 的 $\text{[math]}$ 放置在刻度尺上，求 $\text{[math]}$ 与尺上沿的交点C在尺上的读数为多少厘米．（结果精确到 $\text{[math]}$ 厘米）

（参考数据 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

解答题普通