1.
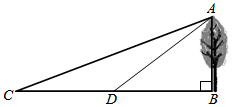
如图,树 垂直于地面,为测树高,小华在
垂直于地面,为测树高,小华在 处测得
处测得 , 然后他沿
, 然后他沿 方向走了
方向走了 米,到达
米,到达 处,测得
处,测得 , 你能帮助小华计算出树的高度吗?
, 你能帮助小华计算出树的高度吗?
【考点】
等腰三角形的性质;
含30°角的直角三角形;
基础巩固
能力提升
变式训练
拓展培优
真题演练