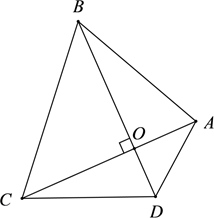1.
对于特殊四边形,通常从定义、性质、判定、应用等方面进行研究,我们借助于这种研究的过程与方法来研究一种新的四边形——筝形.
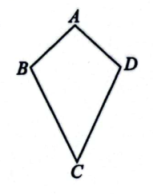
定义:在四边形中,若
, 我们把这样四边形
称为筝形.
性质:按下列分类用文字语言填写相应的性质:
从对称性看:筝形是一个轴对称图形,它的对称轴是;
从边看:筝形有两组邻边分别相等;
从角看:;
从对角线看:.
判定:按要求用文字语言填写相应的判定方法,补全图形,并完成方法2的证明.
方法1:从边看:运用筝形的定义;
方法2:从对角线看:;
如图,四边形中,.求证:四边形
是筝形.
应用:如图,探索筝形的面积公式(直接写出结论).
【考点】
定义新运算;
基础巩固
能力提升
变式训练
拓展培优
真题演练