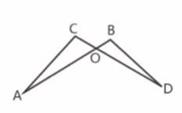
1.
已知点Р是等边△ABC的边BC上的一点，若∠APC=104°，则在以线段AP，BP，CP为边的三角形中，最小内角的大小为（ ）
A.
14°
B.
16°
C.
24°
D.
26°
【考点】
等边三角形的判定与性质;
平行四边形的判定与性质;
