1.

(1)
问题探究:一条线段沿某个方向平移一段距离后与原线段构成一个平行四边形.我们可以利用这一性质,将有些条件通过平移集中在一起来解决一些几何问题.
(2)
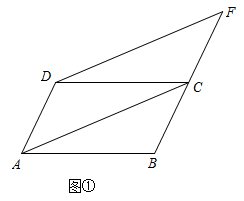
问题解决:如图②,若△ABC中,∠A=90°,点D , 点E分别在AC , AB上,BD交CE于点O , ∠BOC=120°,BD=CE , BE=12,CD=9,求线段BD的长;
(3)
拓展应用:如图③,△ABC中,∠A=45°,D , E分别在AC , AB上,BD , CE交于点O , 若BD=CE , ∠BOC=120°,BE= , CD=5,求BD长.
, CD=5,求BD长.
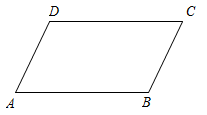
如图①,两条长度相等的线段AB和CD相交于O点,∠AOC=60°,试说明线段AC+BD≥AB .
分析:考虑通过平移,将AC、BD和AB集中到同一个三角形中,运用三角形的三边关系来证明.
如图①,作CE∥AB且CE=AB , 则四边形ABEC是 ▲ (填四边形ABEC的形状),
∴AC=BE;
∵CD=AB=CE , ∠ECD=∠AOC=60°,
∴△DCE是 ▲ (填△DCE的形状),
∴ED=CE=AB.
当AC与BD不平行时,E , B , D三点不在同一直线上,
由三角形三边关系可知,BE+BD ▲ DE(填>或=或<);
当AC∥BD时,E , B , D三点在同一直线上,此时,BE+BD=DE ,
∴AC+BD≥AB .
【考点】
等边三角形的判定与性质;
勾股定理;
平行四边形的判定与性质;
等腰直角三角形;
能力提升