1.
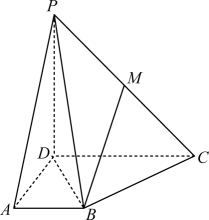
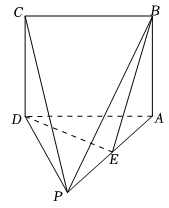
如图,在长方体 中,E , M , N分别是
中,E , M , N分别是 ,
,  ,
,  的中点,
的中点, ,
,  .
.

(1)
求证: ∥平面
∥平面 ;
(2)
试确定直线
;
(2)
试确定直线 与平面
与平面 的交点F的位置,并求
的交点F的位置,并求 的长.
的长.
【考点】
用空间向量研究直线与平面的位置关系;