1.
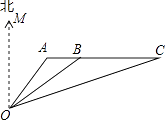
图1是放置在水平面上的可折叠式护眼灯,其中底座的高AB=5 cm,连杆BC=30 cm,灯罩CD=20 cm.如图2,转动BC、CD , 使得∠BCD成平角,且灯罩端点D离桌面l的高度DH为45 cm,求A、H的距离.

【考点】
勾股定理的应用;