1.
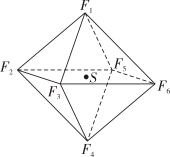
六氟化硫,化学式为 , 在常压下是一种无色、无毒、不燃的稳定气体,有良好的绝缘性,在电器工业方面具有广泛用途.如图所示,其分子结构是六个氟原子处于顶点位置,而硫原子处于中心位置的正八面体,也可将其六个顶点看作正方体各个面的中心点.若正八面体的表面积为
, 在常压下是一种无色、无毒、不燃的稳定气体,有良好的绝缘性,在电器工业方面具有广泛用途.如图所示,其分子结构是六个氟原子处于顶点位置,而硫原子处于中心位置的正八面体,也可将其六个顶点看作正方体各个面的中心点.若正八面体的表面积为 , 则正八面体外接球的体积为( )
, 则正八面体外接球的体积为( )
A.
 B.
B.
 C.
C.
 D.
D.

【考点】
球的表面积与体积公式及应用;
球内接多面体;



