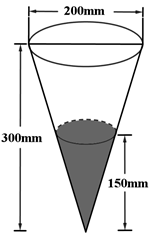
1.
如图,生活中有很多球缺状的建筑.球被平面截下的部分叫做球缺,截面叫做球缺的底面,球缺的曲面部分叫做球冠,垂直于截面的直径被截后的线段叫做球缺的高.球冠面积公式为 , 球缺的体积公式为
, 球缺的体积公式为 , 其中R为球的半径,H为球缺的高.现有一个球被一平面所截形成两个球缺,若两个球冠的面积之比为
, 其中R为球的半径,H为球缺的高.现有一个球被一平面所截形成两个球缺,若两个球冠的面积之比为 , 则这两个球缺的体积之比为( )
, 则这两个球缺的体积之比为( )

A.
 B.
B.
 C.
C.
 D.
D.

【考点】
旋转体(圆柱/圆锥/圆台/球)的结构特征;
基础巩固
能力提升
变式训练
拓展培优
真题演练