1.


(1)
【问题发现】
(2)
【问题提出】
(3)
【问题解决】
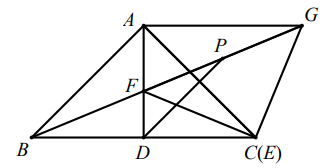
如图 ,
与
中,
,
,
、
、
三点在同一直线上,
,
, 则
.
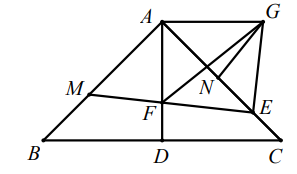
如图 , 在
中,
,
, 过点
作
, 且
, 求
的面积.
如图 , 四边形
中,
,
面积为
且
的长为
, 求
的面积.
【考点】
三角形全等的判定;
等腰直角三角形;